Desarrollaremos técnicas que nos permitirán emplear las fórmulas básicas con objeto de llegar a integrales indefinidas de funciones más complicadas.
Integrales por sustitución
Si u=g(x) es una función diferenciable cuyo recorrido es un intervalo I y f es continua en I,
∫ f (g(x))g´(x)dx = ∫ f (u)du
La regla de sustitución para integrar corresponde a la regla de la cadena para diferenciar. Debemos tener presente que si u=g(x), entonces du=g´(x)dx.
En el cálculo de estas dos integrales:
Si la variable x se reemplaza por una función u(x), para que la integral se calcule sustituyendo u(x) por x, en el integrando debe aparecer u'(x) multiplicando a u(x)α, es decir
En general, si partimos de una integral conocida
y cambiamos la variable x por la función derivable u(x), tal que u'(x) es continua, obtenemos la formula de sutitución:
Si en la fórmula anterior escribimos u = u(x) y u'(x)dx = du, la fórmula de cambio de variable nos quedaría como:
En todos los ejemplos que veremos a continuación, trataremos de reducir el grado de dificultad de la integral mediante un cambio de variable, de tal manera que la integral resultante sea más fácil de integrar ó que sea una integral conocida. Para que la fórmula de cambio de variable tenga posibilidades de éxito, debemos identificar en el integrando a una función u y a u', su derivada.
Ejemplos
Encontrar ∫(3x − 5)4dx
En este caso sencillo podemos observar que esta integral "se parece" a ∫u du 4 , lo cual nos sugiere tomar el cambio de variable u = 3x-5 u = 3x-5 ⇒ du = 3 dx ⇒ dx = (1/3)du
u = 3x-5 ⇒ du = 3 dx ⇒ dx = (1/3)du
Sustituyendo en la integral,
Encontrar
En este caso podemos observar que esta integral "se parece" a ∫u du4 , lo cual nos sugiere tomar el cambio de variable u = cosx
u = cosx ⇒ du = -senx dx ⇒ senx dx = -du
Sustituyendo en la integral,
La presencia de la función lnx y su derivada 1/x, lo cual nos sugiere tomar el cambio de variable: u = lnx ⇒ du = dx/x, sustituyendo en la integral,
A su vez esta integral tendría que resolverse por cambio de variable, tomando w = 3u-5, como se hizo en el ejemplo 1, obteniendo:
Sin embargo para evitar tomar dos o más cambios de variable, debemos percatarnos de que lo importante es que aparece la expresión 1/x que es la derivada de lnx, que también lo es de (3lnx-5), salvo constantes.
Más precisamente, podemos tomar el cambio de variable: u = 3lnx-5 ⇒ du = 3dx/x, ò bien dx/x = du/3,
y al sustituir en la integral original:
Observación: De lo anterior podemos concluir que el cambio de variable procede cuando en el integrando aparece una función u y su derivada multiplicada por una constante. Además que la integral de la variable u sea posible resolverla.
Encontrar
u = cosx ⇒ du = -senx
Como -ln(cosx) = ln1 - ln(cosx) = ln(1/cosx) = ln(secx), podemos expresar
Análogamente,
u = 3x-5 ⇒ du = 3 dx ⇒ dx = (1/3)du
Sustituyendo en la integral,
Encontrar
En este caso podemos observar que esta integral "se parece" a ∫u du4 , lo cual nos sugiere tomar el cambio de variable u = cosx
u = cosx ⇒ du = -senx dx ⇒ senx dx = -du
Sustituyendo en la integral,
Encontrar
La presencia de la función lnx y su derivada 1/x, lo cual nos sugiere tomar el cambio de variable: u = lnx ⇒ du = dx/x, sustituyendo en la integral,
A su vez esta integral tendría que resolverse por cambio de variable, tomando w = 3u-5, como se hizo en el ejemplo 1, obteniendo:
Sin embargo para evitar tomar dos o más cambios de variable, debemos percatarnos de que lo importante es que aparece la expresión 1/x que es la derivada de lnx, que también lo es de (3lnx-5), salvo constantes.
Más precisamente, podemos tomar el cambio de variable: u = 3lnx-5 ⇒ du = 3dx/x, ò bien dx/x = du/3,
y al sustituir en la integral original:
Observación: De lo anterior podemos concluir que el cambio de variable procede cuando en el integrando aparece una función u y su derivada multiplicada por una constante. Además que la integral de la variable u sea posible resolverla.
Encontrar
En una primera vista no advertimos la presencia de una función u y su derivada, ya que la derivada de 1 + x6 = 6x5 y en el integrando no aparece x5 sino x2. No debemos perder de vista que al hacer un cambio de variable es porque nuestra integral es similar o se puede reducir a otra fácil de resolver. Si pensamos que x2 dx será el nuevo diferencial, entonces u tendría que ser x3, es decir u = x3; du = 3x2 dx como se ve al expresar la integral de la siguiente manera:
Encontar
u = cosx ⇒ du = -senx
Como -ln(cosx) = ln1 - ln(cosx) = ln(1/cosx) = ln(secx), podemos expresar
Análogamente,
Video Tutorial
Ejercicios
Aplicando el método de integración por sustitución, encuentre las integrales indefinidas siguientes:
Integración por partes
Este método nos permitirá resolver integrales de funciones que pueden expresarse como un producto de una función por la derivada de otra. Más precisamente, deduciremos la fórmula de integración por partes a partir de la regla para derivar un producto de dos funciones.
Sean u=f(x) y v = g(x) entonces du=f´(x)dx y dv=g´(x) dx así, según la regla de sustitución, la fórmula de integración por partes se transforma en:
∫udv = uv − ∫ vdu
Ejemplo
Encuentre ∫ x cos(x) dx
Con el fin de utilizar la fórmula anterior, tomaremos f(x) = x y g'(x) = cos(x), es decir el integrando xcos(x) = f(x) g'(x)
f(x) = x g '(x) = cos(x)
f '(x) = 1 g(x) = sen(x)
∫ x cos(x) dx = xsen(x) − ∫ sen(x) dx = − xsen(x) + cos(x) + c
NOTACIÓN. Con el fin de ser congruentes con la notación utilizada en la mayoría de los libros del mercado, le llamaremos u = f(x) y v = g(x) y en consecuencia du = f '(x)dx así como dv = g '(x)dx. Con esta nueva notación resolveremos los siguientes ejercicios.
Encuentre ∫ xex dx
u = x v = ex
du = dx dv = ex dx
Obsérvese que con esta notación, en vez de tomar g' (x) = ex, tomamos su diferencial dv = ekdx y análogamente con f, permitiendo que una parte del integrando sea u y el resto sea dv.
En estos primeros dos ejemplos, una adecuada elección de u y dv nos lleva en un solo paso a resolver nuestra integral reduciéndola a una integral más fácil de resolver. Existen otras situaciones, como se verá en los siguientes ejemplos, en que si bien la integral del lado derecho tiene un menor grado de dificultad, no es una integral inmediata, requiere de un nuevo proceso de integración por partes ó resolverla por cambio de variable, ó algún otro procedimiento.
Encuentre ∫sen2 (x) dx
u = senx v = -cosx
du =cos dx dv = senx dx
du =cos dx dv = senx dx
que al sustituirse nos da:
obteniendo la identidad
en la que si dejamos en el lado izquierdo las integrales, obtenemos 0 = 0, que no nos ayuda a encontrar el valor de nuestra integral. La alternativa en este caso es utilizar la identidad trigonométrica sen2x + cos2x =1 inmediatamente después de la primera integración por partes.
Si bien nos vuelve a aparecer la misma integral, esta vez aparece con distinto signo, lo que nos permite despejarla, es decir si dejamos del lado izquierdo las integrales, obtendremos:
Encuentre
Video Tutorial
Ejercicios
Determine las siguientes integrales utilizando el método de integración por partes:
Integrales de funciones trigonómetricas
A continuación veremos algunas reglas para integrar cierto tipo de funciones trigonométricas, que posteriormente se utilizarán en el método de sustitución trigonométrica.
Las identidades trigonométricas nos servirán para integrar ciertas combinaciones de funciones trigonométricas.
Productos de potencias de senos y cosenos
a) Si m y n son pares, utilizaremos las identidades:
b) Si m ó n es impar, utilizaremos la identidad:
Productos de potencias de tangentes y secantes
a) Si n es par, utilizamos la identidad:
b) Si m es impar, utilizamos la identidad:
c) Si n es impar y m par usamos algún otro método como por ejemplo integración por partes.
¿Cómo calculamos las integrales del tipo ∫ senmx cos nxdx ?
Para evaluar las integrales:
se emplean las identidades correspondientes:
Ejemplos
Resolver:
Solución:
Sea u = cosx, entonces du = -senx, y al sustituir en la integral obtenemos:
Resolver:
Solución:
sea u = senx, entonces du = cosx, y al sustituir en la integral obtenemos:
Resolver:
Solución:





































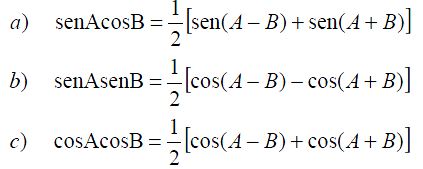








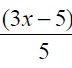


0 comentarios:
Publicar un comentario