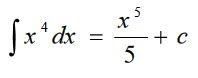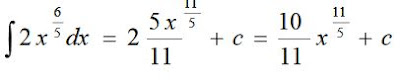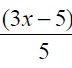MÉTODOS DE INTEGRACIÓN

Desarrollaremos técnicas que nos permitirán emplear las fórmulas básicas con objeto de llegar a integrales indefinidas de funciones más complicadas.

CONCEPTO DE INTEGRAL

La antiderivada

Una forma de ver la operación inversa de la derivación, clásicamente, se realiza de la siguiente forma:

Encontrar la función f(x) de la cual derivada es conocida. Dada la diferencial de la función df(x) encontrar la función f(x)

La función que se pide se le conoce como integral de la diferencial dada y al procedimiento utilizado para encontrar la integral se le conoce como integración. Al igual que el símbolo de derivada, el símbolo de integración, cuyo operador nos indicara la operación mencionada, ha tenido toda una evolución que fue acompañado de rasgos históricos hasta llegar a símbolo







Concretamente diremos que:

Aunque esta relación no es del todo general es correcta y nos será útil para incursionar el análisis de este concepto. Así por ejemplo podemos tener f1(x)= 3x y con ello f1´(x)dx=3dx por lo que




Pero podemos observar que si la función es f2(x)= 3x+5= f1(x)+5 entonces f2´(x)dx=3dx por lo que:




Podemos entonces pensar que en general pudimos agregar a f1(x) cualquier constante y tener el mismo diferencial por lo que una expresión mas general a considerar es la siguiente:




A la constante c que se agrega se le conoce como constante de integración. A la expresión anterior se le conoce como integral indefinida. Retomemos el ejemplo:




Que sucede si aplicamos el operador de derivadas en ambos miembros de la expresión:





Lo que hace pensar que al aplicar el operador de derivada al operador de Integración obtenemos la función a integrar. De forma mas general tendremos:







Como podemos observar el operador de derivada en una operador inverso al de integración, hemos concluido esto en base a la expresión anterior. Sin embargo, si el operador de integral antecede al símbolo de derivada la expresión no siempre será cierta, y en ocasiones, no siempre podremos obtener una solución.

Tabla de integrales

Video Tutorial

Ejemplos

∫ -9dx = -9x + C
∫ 1/8dx = 1/8x + C
∫ πdx = πx + C
∫ 52dx = 52x + C

Integral de una suma o resta de funciones:

entonces integrando cada termino se tiene:

Ejercicios Propuestos

CÁLCULO

El Cálculo, rama de las matemáticas que se ocupa del estudio de los incrementos en las variables, pendientes de curvas, valores máximo y mínimo de funciones y de la determinación de longitudes, áreas y volúmenes. Su uso es muy extenso, sobre todo en ciencias e ingeniería, siempre que haya cantidades que varíen de forma continua.

El cálculo integral emergió de la necesidad de solucionar el problema de la obtención de áreas de figuras planas. Los griegos lo abordaron, llegando a fórmulas para el área de polígonos, círculo, segmentos de parábolas, etc. El método que utilizaron consistía en aproximar al máximo la figura cuya área se quería calcular mediante polígonos de áreas conocidas.

Este procedimiento original de Eudoxo (406 a.C. - 355 a.C.) fue utilizado Euclides (300 a.C.) y por Arquímedes (286 a.C. - 212 a.C.).

Hacia el siglo XVI, este método comenzó a llamarse método de exhaución o método exhaustivo. Basándose en ese método, los matemáticos del siglo XVII implantaron el concepto más general de integral definida de una función, f, en un intervalo. Este concepto fue posteriormente mejorado por Cauchy (1789-1857) y por Riemann (1826 - 1866). Ver integral de Rieman.